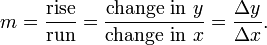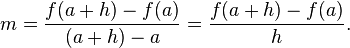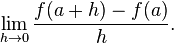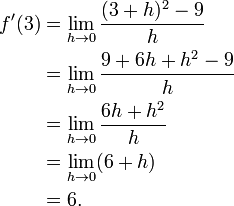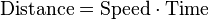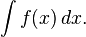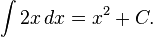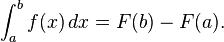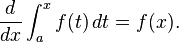Ang section mi xempre may mga babae man... 26 sinda gabos.. tapos iba iba man ang personality ninda.. tapos pag pinagsama sama mo sinda, medyo maribok yan(garo sa kami dai maribok..hahaha) pero enjoyun yan...hehehe.. ididiscribe ko man cnda base sa pagkakabisto ko sainda.. Alphabetical man xempz..
Pearl Alvhie Asis
-iniyo ang seatmate ko... may eyeglasses siya.. malabo siguro ang mata nya..hahaha.. maboot yan xempz dawa pirmi yan iniiwal ayos lang saiya..
Claire Barbosa
-harani man ang tinutukawan niya sa may tinutukawan ko... Medyo may pagka icp aki yan..hehehe.. pero sa totoo, aki pa man talga yan.
Marion Joyce Barbosa
-ini man ang pambato kang section mi pag may beauty contest.. Pirang beses na man yan nanggana... pinaka huri tong miss hayskol.. astig ano??hehe... Maugma pati siyang kajamming..
Maria Ava Barrammeda
-harani man ini sa seat ko.. kaibanan mi man pati siya sa kalokohan.. matibay man pati yan sa mga bagay bagay... dai nalang nindo aramon kung sain..hahaha..
Ruby Bengoa
-medyo harayo na siya sa seat ko pero kabali man siya sa mga jamming mi.. tapos pag yan ang mangtrip siguradong mapangiritun..hahaha.. kaya kung habo mong ngiritan dai mo siya iwalun.. dai man kaya siya nangiiwal pag dai mo ma siya iiwalun.
Melanie Betangcor
-saro man siya sa mga jolly persons sa room, medyo maribok man pati yan.. pero maboot xempz..hehehe...
Jessalyn Blacer
-kataid siya kang sarong jolly person kaya masayahin man siya.. dai pati yan paraiwal.. minsan inaagi nalang kayan sa hibi ang kaanggotan niya sa sarong tao.. pero bako man yan reason para iwalon siya ano????hehehe
Maureen Briones
-saro naman ni sa mga malulupet kong friends.. enjoyon kea yan mangtrip kaya astigun... dai pati yan madaling maanggot..hhehe.. may magayon na ugali, magalang, saka matalino pa... kaya may taong crush na crush siya..hahaha
Abegail Buela
-enjoy man niyong kaibanan... makaraw man.... tapos emo..hahaha... kaya ngani mahirap eexplain yan taong yan..hahaha
Diana Cuibillas
-saro niyo sa mga taong nakakaaram ning dakol tungkol sako.. in short, best friend... dai pati kayan pinagkakalat mga secrets ko... minsan pati nagkakaproblema yan dahil sako..
Lilian Rose de Lara
-medyo dai ko siya nakakaisturyahan kaya mahirap para sako na ediscribe siya... kaya no comment nalang...hahaha
Dyannara Dela Rosa
-kabatch ko ini sa central medyo dai man kami nagisistoryahan kaya no comment ulit...hahaha
Rizzavic Espera
- medyo dai man kami nagisistoryahan kaya no comment ulit...hahaha
Romila Garcia
-saro man siya sa mga honors samo.. maaapod man siyang "all-around" na estudyante... matibay siya sa sports, sa science saka kung sain sain pa...
Axel Gayondato
-saro man siya sa mga honors samo... masayahin man siya..hahahaha.. responsable, tapos maboot..hahaha
Carmela Labe
-matrip man niyong taong iniyo... "MABOOT" man yan... "MAPAGBIGAY" pa...hahaha
Melanie Manere
-matibay ini sa dakol na bagay, sa math, science, saka sa paggibo ning designs para sa mga bulletin mi
Renz Marie Nollase
-barkada niyo kang mga matitrip na tao kaya matrip na man yan... enjoy man yan kajamming..
Grace Vernadeth Oaquira
-saro man niyo sa mga pinaka tahimik samo sa klase.. inda kung tano dai siya nahahawa kay renz..hehehe... pero maboot yan... magayon pati ang surat kayan....hahaha...
Ma. Eliza Oporto
-saro man niyo sa pinakamasayahin samo.. madali lang pati siyang pakisamahan.. medyo prangka siya magtaram.. pero ayos man lang..hahaha..
Ana Marie Pamor
-ini na siguro ang pinaka maboot samo sa room... responsable, dai naaanggot, galante saka matalino..kaya ngani siya ang pres. mi..
Chesa Mae San Pascual
-no comment!!!!hahaha
Joanna-Grace Saraspi
-ini man ang pambato mi sa Filipino... sa klase mi, siya lang ang member ng Haligi ng Wika.. V-pres pa ngani sa General officer.
Sharmaine Sto. Domingo
-medyo dai man kami nagisistoryahan kaya no comment ulit...hahaha
Vibien Tawing
-saro man daa ning emo..hahaha.. mayo na akong ibang masabi ta "confedencial".hahaha.
Misna Zurbano
-medyo dai man kami nagisistoryahan kaya no comment ulit...hahaha
Hay salamat natapos na... Banggihun na naman... dai man sana maanggot c mama ko..hahaha.. Pati man daa c diana ta hinalat nya man daa ako..hahaha....
Thursday, August 27, 2009
Classmates
Saturday, August 22, 2009
Classmates
Ang samuyang section ay pano kang mga mauurag asin "maboboot" na tao..hahaha
Pero dawa arog sinda ka iyan ayos lang.. Enjoy ang highschool life dahil sainda..
May itatao akong discription ninda kada saro... Sana mayo man maanggot..hahaha
Sasaro-saroun ko sinda.. alphabetically.. puon sa boys....hahaha
Rimar Ariñabo
-Saro siya sa pinaka barkada ko.. Medyo pilyo yan... Madalas pati kaming magkaigwa ning iwal ta sa kapasawayan ka iyan... Pero madali man lang.. kaya in general magayon siyang barkada..
Jeric Basallote
-Iniyong taong iniyo magayonun maging barkada talga... Enjoyun ining kaibanan.. Lalo na sa kalokohan...hahahaha.. kung siya ang magjoke inda ko lang kung dai ka magngirit..hahahaha.. Saro lang ang masasabi ko saiya, Mayo akong masabi!..hahaha
Christian Capistrano
-Saro man yan sa mga kakawat ko.. lalo na sa DOTA...haha... Tibayun yan... Siya kaya ang nagtukdo sakong magDOTA.. Enjoy yan kakawat, dawa nakakapikon kung minsan...
Benigno Esguerra III
-Pangaran palang, gwapo na..hahaha.. pero sa personal gwapo talaga yan.. Matalino pati yan... Lalo sa Math.. Tapos responsable.. May paninindigan.. medyo masungit lang.. Pero ayos siyang maging barkada..
Jay-ar Fernandez
-Saro siya sa mga "all around" sa room mi... Halos matibay siya sa gabos... Sa Math, Science, name it, sigurado may ibubuga yan... Maboot pati yan, responsable pa... kaya ngani kabali siya sa honors mi...hahaha.. In general, IDOL siya...hahaha
Bernard John Hermida
-Ini man, matibay siya sa kadakul na bagay, maugmahon man pati siya. Dawa tigpaparatripan mi yan ayos lang saiya..hahaha. Bihira lang ang taong arug sa iya....
Paul John Legaspi
-Ini man taong iniyo, medyo tahimik man yan.. Pambato mi pati yan sa mga contest. sa iba-ibang contest. dakol pati yang taga hanga..hahahaha..
John Micheal Mariquit
-Ini ang sarong taong maaapod na "_______" aram ko kayang pag inapod ko siyang arug ka iyan, maaanggot to.. Medyo may pagka "weird" lang ang ugali niya.. Pero ayos man yan maging barkada.
Meyer Marquez
-Saro man siya sa mga matitibay samo sa Math..hahahaha.. Sige pati yan tukdo sa mga classmates ming dai masyadong naintindihan ang lesson.. Matibay man palan yan sa PHYSICS..hahaha.. Medyo masakit kaya ang physics. Lalo na ang magtuom mga formula...hahaha
Rene Irvin Pasiona
-Saro siya sa mga responsableng estudyante samo.. Medyo makaraw yan..hahahaha.. Lalo na kung may baraylehan....hahaha... Maboot pati yan..
Marlon Patoc
-Ini ang pinaka matangkad samo..hahaha.. inda ko man kung ano ang paparakakan niya kung tano siya arug kato kalangkaw...hahaha
Jeric Perez
-Saro man siya sa mga barkada ko... Sabay pait ang bday ming duwa.. astigun ano???hahaha.. Makaraw man pati siya..
Jan Marvin Rosales
-Ini man taong iniyo, tahimik man daa..hahaha.. pero saru na manyan samo.. maloko naman yan...
Jose Charles San Agustin
-Ako na niyo..hahaha Mayo man akong masabi..hahaha...
Thursday, August 20, 2009
Calculus
Pinaka masakit na math...hahahaha..
Sa wikipedia ko palan nakua ang mga infos na niu...hahaha
Calculus (Latin, calculus, a small stone used for counting) is a discipline in mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern university education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem of calculus. Calculus is the study of change, in the same way that geometry is the study of shape and algebra is the study of equations. A course in calculus is a gateway to other, more advanced courses in mathematics devoted to the study of functions and limits, broadly called mathematical analysis. Calculus has widespread applications in science, economics, and engineering and can solve many problems for which algebra alone is insufficient.
Historically, calculus was called "the calculus of infinitesimals", or "infinitesimal calculus". More generally, calculus (plural calculi) may refer to any method or system of calculation guided by the symbolic manipulation of expressions. Some examples of other well-known calculi are propositional calculus, variational calculus, lambda calculus, pi calculus and join calculus.
Ancient
The ancient period introduced some of the ideas of integral calculus, but does not seem to have developed these ideas in a rigorous or systematic way. Calculating volumes and areas, the basic function of integral calculus, can be traced back to the Egyptian Moscow papyrus (c. 1820 BC), in which an Egyptian successfully calculated the volume of a pyramidal frustum.[1][2] From the school of Greek mathematics, Eudoxus (c. 408−355 BC) used the method of exhaustion, which prefigures the concept of the limit, to calculate areas and volumes while Archimedes (c. 287−212 BC) developed this idea further, inventing heuristics which resemble integral calculus.[3] The method of exhaustion was later used in China by Liu Hui in the 3rd century AD in order to find the area of a circle. In the 5th century AD, Zu Chongzhi used what would later be called Cavalieri's principle to find the volume of a sphere.[2]
Medieval
Around AD 1000, the Islamic mathematician, Ibn al-Haytham (Alhacen), was the first to derive the formula for the sum of the fourth powers of an arithmetic progression, using a method that is readily generalizable to finding the formula for the sum of any higher integral powers, which he used to perform an integration.[4] In the 11th century, the Chinese polymath Shen Kuo developed 'packing' equations that dealt with integration. In the 12th century, the Indian mathematician, Bhāskara II, developed an early derivative representing infinitesimal change, and he described an early form of Rolle's theorem.[5] Also in the 12th century, the Persian mathematician Sharaf al-Dīn al-Tūsī discovered the derivative of cubic polynomials, an important result in differential calculus.[6] In the 14th century, Madhava of Sangamagrama, along with other mathematician-astronomers of the Kerala school of astronomy and mathematics, described special cases of Taylor series,[7] which are treated in the text Yuktibhasa.[8][9][10]
Modern
In the modern period, independent discoveries relating to calculus were being made in early 17th century Japan, by mathematicians such as Seki Kowa, who expanded upon the method of exhaustion.
In Europe, the foundational work was a treatise due to Bonaventura Cavalieri, who argued that volumes and areas should be computed as the sums of the volumes and areas of infinitesimal thin cross-sections. The ideas were similar to Archimedes' in The Method, but this treatise was lost until the early part of the twentieth century. Cavalieri's work was not well respected since his methods can lead to erroneous results, and the infinitesimal quantities he introduced were disreputable at first.
The formal study of calculus combined Cavalieri's infinitesimals with the calculus of finite differences developed in Europe at around the same time. The combination was achieved by John Wallis, Isaac Barrow, and James Gregory, the latter two proving the second fundamental theorem of calculus around 1675.
The product rule and chain rule, the notion of higher derivatives, Taylor series, and analytical functions were introduced by Isaac Newton in an idiosyncratic notation which he used to solve problems of mathematical physics. In his publications, Newton rephrased his ideas to suit the mathematical idiom of the time, replacing calculations with infinitesimals by equivalent geometrical arguments which were considered beyond reproach. He used the methods of calculus to solve the problem of planetary motion, the shape of the surface of a rotating fluid, the oblateness of the earth, the motion of a weight sliding on a cycloid, and many other problems discussed in his Principia Mathematica. In other work, he developed series expansions for functions, including fractional and irrational powers, and it was clear that he understood the principles of the Taylor series. He did not publish all these discoveries, and at this time infinitesimal methods were still considered disreputable.
These ideas were systematized into a true calculus of infinitesimals by Gottfried Wilhelm Leibniz, who was originally accused of plagiarism by Newton. He is now regarded as an independent inventor of and contributor to calculus. His contribution was to provide a clear set of rules for manipulating infinitesimal quantities, allowing the computation of second and higher derivatives, and providing the product rule and chain rule, in their differential and integral forms. Unlike Newton, Leibniz paid a lot of attention to the formalism – he often spent days determining appropriate symbols for concepts.
Leibniz and Newton are usually both credited with the invention of calculus. Newton was the first to apply calculus to general physics and Leibniz developed much of the notation used in calculus today. The basic insights that both Newton and Leibniz provided were the laws of differentiation and integration, second and higher derivatives, and the notion of an approximating polynomial series. By Newton's time, the fundamental theorem of calculus was known.
When Newton and Leibniz first published their results, there was great controversy over which mathematician (and therefore which country) deserved credit. Newton derived his results first, but Leibniz published first. Newton claimed Leibniz stole ideas from his unpublished notes, which Newton had shared with a few members of the Royal Society. This controversy divided English-speaking mathematicians from continental mathematicians for many years, to the detriment of English mathematics. A careful examination of the papers of Leibniz and Newton shows that they arrived at their results independently, with Leibniz starting first with integration and Newton with differentiation. Today, both Newton and Leibniz are given credit for developing calculus independently. It is Leibniz, however, who gave the new discipline its name. Newton called his calculus "the science of fluxions".
Since the time of Leibniz and Newton, many mathematicians have contributed to the continuing development of calculus. In the 19th century, calculus was put on a much more rigorous footing by mathematicians such as Cauchy, Riemann, and Weierstrass (see (ε, δ)-definition of limit). It was also during this period that the ideas of calculus were generalized to Euclidean space and the complex plane. Lebesgue generalized the notion of the integral so that virtually any function has an integral, while Laurent Schwartz extended differentiation in much the same way.
Calculus is a ubiquitous topic in most modern high schools and universities, and mathematicians around the world continue to contribute to its development.[11]
Significance
While some of the ideas of calculus were developed earlier in Greece, China, India, Iraq, Persia, and Japan, the modern use of calculus began in Europe, during the 17th century, when Isaac Newton and Gottfried Wilhelm Leibniz built on the work of earlier mathematicians to introduce its basic principles. The development of calculus was built on earlier concepts of instantaneous motion and area underneath curves.
Applications of differential calculus include computations involving velocity and acceleration, the slope of a curve, and optimization. Applications of integral calculus include computations involving area, volume, arc length, center of mass, work, and pressure. More advanced applications include power series and Fourier series. Calculus can be used to compute the trajectory of a shuttle docking at a space station or the amount of snow in a driveway.
Calculus is also used to gain a more precise understanding of the nature of space, time, and motion. For centuries, mathematicians and philosophers wrestled with paradoxes involving division by zero or sums of infinitely many numbers. These questions arise in the study of motion and area. The ancient Greek philosopher Zeno gave several famous examples of such paradoxes. Calculus provides tools, especially the limit and the infinite series, which resolve the paradoxes.
Foundations
In mathematics, foundations refers to the rigorous development of a subject from precise axioms and definitions. Working out a rigorous foundation for calculus occupied mathematicians for much of the century following Newton and Leibniz and is still to some extent an active area of research today.
There is more than one rigorous approach to the foundation of calculus. The usual one today is via the concept of limits defined on the continuum of real numbers. An alternative is nonstandard analysis, in which the real number system is augmented with infinitesimal and infinite numbers, as in the original Newton-Leibniz conception. The foundations of calculus are included in the field of real analysis, which contains full definitions and proofs of the theorems of calculus as well as generalizations such as measure theory and distribution theory.
Principles
Limits and infinitesimals
Calculus is usually developed by manipulating very small quantities. Historically, the first method of doing so was by infinitesimals. These are objects which can be treated like numbers but which are, in some sense, "infinitely small". An infinitesimal number dx could be greater than 0, but less than any number in the sequence 1, ½, ⅓, ... and less than any positive real number. Any integer multiple of an infinitesimal is still infinitely small, i.e., infinitesimals do not satisfy the Archimedean property. From this point of view, calculus is a collection of techniques for manipulating infinitesimals. This approach fell out of favor in the 19th century because it was difficult to make the notion of an infinitesimal precise. However, the concept was revived in the 20th century with the introduction of non-standard analysis and smooth infinitesimal analysis, which provided solid foundations for the manipulation of infinitesimals.
In the 19th century, infinitesimals were replaced by limits. Limits describe the value of a function at a certain input in terms of its values at nearby input. They capture small-scale behavior, just like infinitesimals, but use the ordinary real number system. In this treatment, calculus is a collection of techniques for manipulating certain limits. Infinitesimals get replaced by very small numbers, and the infinitely small behavior of the function is found by taking the limiting behavior for smaller and smaller numbers. Limits are easy to put on rigorous foundations, and for this reason they are usually considered to be the standard approach to calculus.
Differential calculus
Differential calculus is the study of the definition, properties, and applications of the derivative of a function. The process of finding the derivative is called differentiation. Given a function and a point in the domain, the derivative at that point is a way of encoding the small-scale behavior of the function near that point. By finding the derivative of a function at every point in its domain, it is possible to produce a new function, called the derivative function or just the derivative of the original function. In mathematical jargon, the derivative is a linear operator which inputs a function and outputs a second function. This is more abstract than many of the processes studied in elementary algebra, where functions usually input a number and output another number. For example, if the doubling function is given the input three, then it outputs six, and if the squaring function is given the input three, then it outputs nine. The derivative, however, can take the squaring function as an input. This means that the derivative takes all the information of the squaring function—such as that two is sent to four, three is sent to nine, four is sent to sixteen, and so on—and uses this information to produce another function. (The function it produces turns out to be the doubling function.)
The most common symbol for a derivative is an apostrophe-like mark called prime. Thus, the derivative of the function of f is f′, pronounced "f prime." For instance, if f(x) = x2 is the squaring function, then f′(x) = 2x is the doubling function.
If the input of the function represents time, then the derivative represents change with respect to time. For example, if f is a function that takes a time as input and gives the position of a ball at that time as output, then the derivative of f is how the position is changing in time, that is, it is the velocity of the ball.
If a function is linear (that is, if the graph of the function is a straight line), then the function can be written y = mx + b, where:
This gives an exact value for the slope of a straight line. If the graph of the function is not a straight line, however, then the change in y divided by the change in x varies. Derivatives give an exact meaning to the notion of change in output with respect to change in input. To be concrete, let f be a function, and fix a point a in the domain of f. (a, f(a)) is a point on the graph of the function. If h is a number close to zero, then a + h is a number close to a. Therefore (a + h, f(a + h)) is close to (a, f(a)). The slope between these two points is
This expression is called a difference quotient. A line through two points on a curve is called a secant line, so m is the slope of the secant line between (a, f(a)) and (a + h, f(a + h)). The secant line is only an approximation to the behavior of the function at the point a because it does not account for what happens between a and a + h. It is not possible to discover the behavior at a by setting h to zero because this would require dividing by zero, which is impossible. The derivative is defined by taking the limit as h tends to zero, meaning that it considers the behavior of f for all small values of h and extracts a consistent value for the case when h equals zero:
Geometrically, the derivative is the slope of the tangent line to the graph of f at a. The tangent line is a limit of secant lines just as the derivative is a limit of difference quotients. For this reason, the derivative is sometimes called the slope of the function f.
Here is a particular example, the derivative of the squaring function at the input 3. Let f(x) = x2 be the squaring function.
The slope of tangent line to the squaring function at the point (3,9) is 6, that is to say, it is going up six times as fast as it is going to the right. The limit process just described can be performed for any point in the domain of the squaring function. This defines the derivative function of the squaring function, or just the derivative of the squaring function for short. A similar computation to the one above shows that the derivative of the squaring function is the doubling function.
Leibniz notation
A common notation, introduced by Leibniz, for the derivative in the example above is
In an approach based on limits, the symbol dy/dx is to be interpreted not as the quotient of two numbers but as a shorthand for the limit computed above. Leibniz, however, did intend it to represent the quotient of two infinitesimally small numbers, dy being the infinitesimally small change in y caused by an infinitesimally small change dx applied to x. We can also think of d/dx as a differentiation operator, which takes a function as an input and gives another function, the derivative, as the output. For example:
In this usage, the dx in the denominator is read as "with respect to x." Even when calculus is developed using limits rather than infinitesimals, it is common to manipulate symbols like dx and dy as if they were real numbers; although it is possible to avoid such manipulations, they are sometimes notationally convenient in expressing operations such as the total derivative.
Integral calculus
Integral calculus is the study of the definitions, properties, and applications of two related concepts, the indefinite integral and the definite integral. The process of finding the value of an integral is called integration. In technical language, integral calculus studies two related linear operators.
The indefinite integral is the antiderivative, the inverse operation to the derivative. F is an indefinite integral of f when f is a derivative of F. (This use of upper- and lower-case letters for a function and its indefinite integral is common in calculus.)
The definite integral inputs a function and outputs a number, which gives the area between the graph of the input and the x-axis. The technical definition of the definite integral is the limit of a sum of areas of rectangles, called a Riemann sum.
A motivating example is the distances traveled in a given time.
If the speed is constant, only multiplication is needed, but if the speed changes, then we need a more powerful method of finding the distance. One such method is to approximate the distance traveled by breaking up the time into many short intervals of time, then multiplying the time elapsed in each interval by one of the speeds in that interval, and then taking the sum (a Riemann sum) of the approximate distance traveled in each interval. The basic idea is that if only a short time elapses, then the speed will stay more or less the same. However, a Riemann sum only gives an approximation of the distance traveled. We must take the limit of all such Riemann sums to find the exact distance traveled.
If f(x) in the diagram on the left represents speed as it varies over time, the distance traveled (between the times represented by a and b) is the area of the shaded region s.
To approximate that area, an intuitive method would be to divide up the distance between a and b into a number of equal segments, the length of each segment represented by the symbol Δx. For each small segment, we can choose one value of the function f(x). Call that value h. Then the area of the rectangle with base Δx and height h gives the distance (time Δx multiplied by speed h) traveled in that segment. Associated with each segment is the average value of the function above it, f(x)=h. The sum of all such rectangles gives an approximation of the area between the axis and the curve, which is an approximation of the total distance traveled. A smaller value for Δx will give more rectangles and in most cases a better approximation, but for an exact answer we need to take a limit as Δx approaches zero.
The symbol of integration is 
, an elongated S (the S stands for "sum"). The definite integral is written as:
and is read "the integral from a to b of f-of-x with respect to x." The Leibniz notation dx is intended to suggest dividing the area under the curve into an infinite number of rectangles, so that their width Δx becomes the infinitesimally small dx. In a formulation of the calculus based on limits, the notation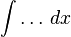 
is to be understood as an operator that takes a function as an input and gives a number, the area, as an output; dx is not a number, and is not being multiplied by f(x).
The indefinite integral, or antiderivative, is written:
Functions differing by only a constant have the same derivative, and therefore the antiderivative of a given function is actually a family of functions differing only by a constant. Since the derivative of the function y = x² + C, where C is any constant, is y′ = 2x, the antiderivative of the latter is given by:
An undetermined constant like C in the antiderivative is known as a constant of integration.
Fundamental theorem
The fundamental theorem of calculus states that differentiation and integration are inverse operations. More precisely, it relates the values of antiderivatives to definite integrals. Because it is usually easier to compute an antiderivative than to apply the definition of a definite integral, the Fundamental Theorem of Calculus provides a practical way of computing definite integrals. It can also be interpreted as a precise statement of the fact that differentiation is the inverse of integration.
The Fundamental Theorem of Calculus states: If a function f is continuous on the interval [a, b] and if F is a function whose derivative is f on the interval (a, b), then
Furthermore, for every x in the interval (a, b),
This realization, made by both Newton and Leibniz, who based their results on earlier work by Isaac Barrow, was key to the massive proliferation of analytic results after their work became known. The fundamental theorem provides an algebraic method of computing many definite integrals—without performing limit processes—by finding formulas for antiderivatives. It is also a prototype solution of a differential equation. Differential equations relate an unknown function to its derivatives, and are ubiquitous in the sciences.
Applications
Calculus is used in every branch of the physical sciences, in computer science, statistics, engineering, economics, business, medicine, demography, and in other fields wherever a problem can be mathematically modeled and an optimal solution is desired.
Physics makes particular use of calculus; all concepts in classical mechanics are interrelated through calculus. The mass of an object of known density, the moment of inertia of objects, as well as the total energy of an object within a conservative field can be found by the use of calculus. In the subfields of electricity and magnetism calculus can be used to find the total flux of electromagnetic fields. A more historical example of the use of calculus in physics is Newton's second law of motion, it expressly uses the term "rate of change" which refers to the derivative: The rate of change of momentum of a body is equal to the resultant force acting on the body and is in the same direction. Even the common expression of Newton's second law as Force = Mass × Acceleration involves differential calculus because acceleration can be expressed as the derivative of velocity. Maxwell's theory of electromagnetism and Einstein's theory of general relativity are also expressed in the language of differential calculus. Chemistry also uses calculus in determining reaction rates and radioactive decay.
Calculus can be used in conjunction with other mathematical disciplines. For example, it can be used with linear algebra to find the "best fit" linear approximation for a set of points in a domain. Or it can be used in probability theory to determine the probability of a continuous random variable from an assumed density function.
Green's Theorem, which gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C, is applied in an instrument known as a planimeter which is used to calculate the area of a flat surface on a drawing. For example, it can be used to calculate the amount of area taken up by an irregularly shaped flower bed or swimming pool when designing the layout of a piece of property.
In the realm of medicine, calculus can be used to find the optimal branching angle of a blood vessel so as to maximize flow.
In analytic geometry, the study of graphs of functions, calculus is used to find high points and low points (maxima and minima), slope, concavity and inflection points.
In economics, calculus allows for the determination of maximal profit by providing a way to easily calculate both marginal cost and marginal revenue.
Calculus can be used to find approximate solutions to equations, in methods such as Newton's method, fixed point iteration, and linear approximation. For instance, spacecraft use a variation of the Euler method to approximate curved courses within zero gravity environments.
Geometry
Hay... Kung bako lang math ang paborito ko...hahaha
Geometry (Ancient Greek: γεωμετρία; geo = earth, metria = measure) is a part of mathematics concerned with questions of size, shape, and relative position of figures and with properties of space. Geometry is one of the oldest sciences. Initially a body of practical knowledge concerning lengths, areas, and volumes, in the third century BC geometry was put into an axiomatic form by Euclid, whose treatment—Euclidean geometry—set a standard for many centuries to follow. The field of astronomy, especially mapping the positions of the stars and planets on the celestial sphere, served as an important source of geometric problems during the next one and a half millennia. A mathematician who works in the field of geometry is called a geometer.
Introduction of coordinates by René Descartes and the concurrent development of algebra marked a new stage for geometry, since geometric figures, such as plane curves, could now be represented analytically, i.e., with functions and equations. This played a key role in the emergence of calculus in the 17th century. Furthermore, the theory of perspective showed that there is more to geometry than just the metric properties of figures. The subject of geometry was further enriched by the study of intrinsic structure of geometric objects that originated with Euler and Gauss and led to the creation of topology and differential geometry.
Since the 19th century discovery of non-Euclidean geometry, the concept of space has undergone a radical transformation. Contemporary geometry considers manifolds, spaces that are considerably more abstract than the familiar Euclidean space, which they only approximately resemble at small scales. These spaces may be endowed with additional structure, allowing one to speak about length. Modern geometry has multiple strong bonds with physics, exemplified by the ties between Riemannian geometry and general relativity. One of the youngest physical theories, string theory, is also very geometric in flavour.
The visual nature of geometry makes it initially more accessible than other parts of mathematics, such as algebra or number theory. However, the geometric language is also used in contexts that are far removed from its traditional, Euclidean provenance, for example, in fractal geometry, and especially in algebraic geometry.[1]
Practical geometry
There is little doubt that geometry originated as a practical science, concerned with surveying, measurements, areas, and volumes. Among the notable accomplishments one finds formulas for lengths, areas and volumes, such as Pythagorean theorem, circumference and area of a circle, area of a triangle, volume of a cylinder, sphere, and a pyramid. Development of astronomy led to emergence of trigonometry and spherical trigonometry, together with the attendant computational techniques.Axiomatic geometry
A method of computing certain inaccessible distances or heights based on similarity of geometric figures and attributed to Thales presaged more abstract approach to geometry taken by Euclid in his Elements, one of the most influential books ever written. Euclid introduced certain axioms, or postulates, expressing primary or self-evident properties of points, lines, and planes. He proceeded to rigorously deduce other properties by mathematical reasoning. The characteristic feature of Euclid's approach to geometry was its rigor. In the 20th century, David Hilbert employed axiomatic reasoning in his attempt to update Euclid and provide modern foundations of geometry.
Geometric constructions
Ancient scientists paid special attention to constructing geometric objects that had been described in some other way. Classical instruments allowed in geometric constructions are those with compass and straightedge. However, some problems turned out to be difficult or impossible to solve by these means alone, and ingenious constructions using parabolas and other curves, as well as mechanical devices, were found. The approach to geometric problems with geometric or mechanical means is known as synthetic geometry.
Numbers in geometry
Already Pythagoreans considered the role of numbers in geometry. However, the discovery of incommensurable lengths, which contradicted their philosophical views, made them abandon (abstract) numbers in favour of (concrete) geometric quantities, such as length and area of figures. Numbers were reintroduced into geometry in the form of coordinates by Descartes, who realized that the study of geometric shapes can be facilitated by their algebraic representation. Analytic geometry applies methods of algebra to geometric questions, typically by relating geometric curves and algebraic equations. These ideas played a key role in the development of calculus in the 17th century and led to discovery of many new properties of plane curves. Modern algebraic geometry considers similar questions on a vastly more abstract level.
Geometry of position
Even in ancient times, geometers considered questions of relative position or spatial relationship of geometric figures and shapes. Some examples are given by inscribed and circumscribed circles of polygons, lines intersecting and tangent to conic sections, the Pappus and Menelaus configurations of points and lines. In the Middle Ages new and more complicated questions of this type were considered: What is the maximum number of spheres simultaneously touching a given sphere of the same radius (kissing number problem)? What is the densest packing of spheres of equal size in space (Kepler conjecture)? Most of these questions involved 'rigid' geometrical shapes, such as lines or spheres. Projective, convex and discrete geometry are three subdisciplines within present day geometry that deal with these and related questions.
A new chapter in Geometria situs was opened by Leonhard Euler, who boldly cast out metric properties of geometric figures and considered their most fundamental geometrical structure based solely on shape. Topology, which grew out of geometry, but turned into a large independent discipline, does not differentiate between objects that can be continuously deformed into each other. The objects may nevertheless retain some geometry, as in the case of hyperbolic knots.
Geometry beyond Euclid
For nearly two thousand years since Euclid, while the range of geometrical questions asked and answered inevitably expanded, basic understanding of space remained essentially the same. Immanuel Kant argued that there is only one, absolute, geometry, which is known to be true a priori by an inner faculty of mind: Euclidean geometry was synthetic a priori.[2] This dominant view was overturned by the revolutionary discovery of non-Euclidean geometry in the works of Gauss (who never published his theory), Bolyai, and Lobachevsky, who demonstrated that ordinary Euclidean space is only one possibility for development of geometry. A broad vision of the subject of geometry was then expressed by Riemann in his inauguration lecture Über die Hypothesen, welche der Geometrie zu Grunde liegen (On the hypotheses on which geometry is based), published only after his death. Riemann's new idea of space proved crucial in Einstein's general relativity theory and Riemannian geometry, which considers very general spaces in which the notion of length is defined, is a mainstay of modern geometry.
Symmetry
The theme of symmetry in geometry is nearly as old as the science of geometry itself. The circle, regular polygons and platonic solids held deep significance for many ancient philosophers and were investigated in detail by the time of Euclid. Symmetric patterns occur in nature and were artistically rendered in a multitude of forms, including the bewildering graphics of M. C. Escher. Nonetheless, it was not until the second half of 19th century that the unifying role of symmetry in foundations of geometry had been recognized. Felix Klein's Erlangen program proclaimed that, in a very precise sense, symmetry, expressed via the notion of a transformation group, determines what geometry is. Symmetry in classical Euclidean geometry is represented by congruences and rigid motions, whereas in projective geometry an analogous role is played by collineations, geometric transformations that take straight lines into straight lines. However it was in the new geometries of Bolyai and Lobachevsky, Riemann, Clifford and Klein, and Sophus Lie that Klein's idea to 'define a geometry via its symmetry group' proved most influential. Both discrete and continuous symmetries play prominent role in geometry, the former in topology and geometric group theory, the latter in Lie theory and Riemannian geometry.
Modern geometry
Modern geometry is the title of a popular textbook by Dubrovin, Novikov, and Fomenko first published in 1979 (in Russian). At close to 1000 pages, the book has one major thread: geometric structures of various types on manifolds and their applications in contemporary theoretical physics. A quarter century after its publication, differential geometry, algebraic geometry, symplectic geometry, and Lie theory presented in the book remain among the most visible areas of modern geometry, with multiple connections with other parts of mathematics and physics.
Contemporary geometers
Some of the representative leading figures in modern geometry are Michael Atiyah, Mikhail Gromov, and William Thurston. The common feature in their work is the use of smooth manifolds as the basic idea of space; they otherwise have rather different directions and interests. Geometry now is, in large part, the study of structures on manifolds that have a geometric meaning, in the sense of the principle of covariance that lies at the root of general relativity theory in theoretical physics. (See Category:Structures on manifolds for a survey.)
Much of this theory relates to the theory of continuous symmetry, or in other words Lie groups. From the foundational point of view, on manifolds and their geometrical structures, important is the concept of pseudogroup, defined formally by Shiing-shen Chern in pursuing ideas introduced by Élie Cartan. A pseudo-group can play the role of a Lie group of 'infinite' dimension.
Dimension
Where the traditional geometry allowed dimensions 1 (a line), 2 (a plane) and 3 (our ambient world conceived of as three-dimensional space), mathematicians have used higher dimensions for nearly two centuries. Dimension has gone through stages of being any natural number n, possibly infinite with the introduction of Hilbert space, and any positive real number in fractal geometry. Dimension theory is a technical area, initially within general topology, that discusses definitions; in common with most mathematical ideas, dimension is now defined rather than an intuition. Connected topological manifolds have a well-defined dimension; this is a theorem (invariance of domain) rather than anything a priori.
The issue of dimension still matters to geometry, in the absence of complete answers to classic questions. Dimensions 3 of space and 4 of space-time are special cases in geometric topology. Dimension 10 or 11 is a key number in string theory. Exactly why is something to which research may bring a satisfactory geometric answer.
Contemporary Euclidean geometry
The study of traditional Euclidean geometry is by no means dead. It is now typically presented as the geometry of Euclidean spaces of any dimension, and of the Euclidean group of rigid motions. The fundamental formulae of geometry, such as the Pythagorean theorem, can be presented in this way for a general inner product space.
Euclidean geometry has become closely connected with computational geometry, computer graphics, convex geometry, discrete geometry, and some areas of combinatorics. Momentum was given to further work on Euclidean geometry and the Euclidean groups by crystallography and the work of H. S. M. Coxeter, and can be seen in theories of Coxeter groups and polytopes. Geometric group theory is an expanding area of the theory of more general discrete groups, drawing on geometric models and algebraic techniques.
Algebraic geometry
The field of algebraic geometry is the modern incarnation of the Cartesian geometry of co-ordinates. After a turbulent period of axiomatization, its foundations are in the twenty-first century on a stable basis. Either one studies the 'classical' case where the spaces are complex manifolds that can be described by algebraic equations; or the scheme theory provides a technically sophisticated theory based on general commutative rings.
The geometric style which was traditionally called the Italian school is now known as birational geometry. It has made progress in the fields of threefolds, singularity theory and moduli spaces, as well as recovering and correcting the bulk of the older results. Objects from algebraic geometry are now commonly applied in string theory, as well as diophantine geometry.
Methods of algebraic geometry rely heavily on sheaf theory and other parts of homological algebra. The Hodge conjecture is an open problem that has gradually taken its place as one of the major questions for mathematicians. For practical applications, Gröbner basis theory and real algebraic geometry are major subfields.
Differential geometry
Differential geometry, which in simple terms is the geometry of curvature, has been of increasing importance to mathematical physics since the suggestion that space is not flat space. Contemporary differential geometry is intrinsic, meaning that space is a manifold and structure is given by a Riemannian metric, or analogue, locally determining a geometry that is variable from point to point.
This approach contrasts with the extrinsic point of view, where curvature means the way a space bends within a larger space. The idea of 'larger' spaces is discarded, and instead manifolds carry vector bundles. Fundamental to this approach is the connection between curvature and characteristic classes, as exemplified by the generalized Gauss-Bonnet theorem.
Topology and geometry
The field of topology, which saw massive development in the 20th century, is in a technical sense a type of transformation geometry, in which transformations are homeomorphisms. This has often been expressed in the form of the dictum 'topology is rubber-sheet geometry'. Contemporary geometric topology and differential topology, and particular subfields such as Morse theory, would be counted by most mathematicians as part of geometry. Algebraic topology and general topology have gone their own ways.
Axiomatic and open development
The model of Euclid's Elements, a connected development of geometry as an axiomatic system, is in a tension with René Descartes's reduction of geometry to algebra by means of a coordinate system. There were many champions of synthetic geometry, Euclid-style development of projective geometry, in the 19th century, Jakob Steiner being a particularly brilliant figure. In contrast to such approaches to geometry as a closed system, culminating in Hilbert's axioms and regarded as of important pedagogic value, most contemporary geometry is a matter of style. Computational synthetic geometry is now a branch of computer algebra.
The Cartesian approach currently predominates, with geometric questions being tackled by tools from other parts of mathematics, and geometric theories being quite open and integrated. This is to be seen in the context of the axiomatization of the whole of pure mathematics, which went on in the period c.1900–c.1950: in principle all methods are on a common axiomatic footing. This reductive approach has had several effects. There is a taxonomic trend, which following Klein and his Erlangen program (a taxonomy based on the subgroup concept) arranges theories according to generalization and specialization. For example affine geometry is more general than Euclidean geometry, and more special than projective geometry. The whole theory of classical groups thereby becomes an aspect of geometry. Their invariant theory, at one point in the nineteenth century taken to be the prospective master geometric theory, is just one aspect of the general representation theory of algebraic groups and Lie groups. Using finite fields, the classical groups give rise to finite groups, intensively studied in relation to the finite simple groups; and associated finite geometry, which has both combinatorial (synthetic) and algebro-geometric (Cartesian) sides.
An example from recent decades is the twistor theory of Roger Penrose, initially an intuitive and synthetic theory, then subsequently shown to be an aspect of sheaf theory on complex manifolds. In contrast, the non-commutative geometry of Alain Connes is a conscious use of geometric language to express phenomena of the theory of von Neumann algebras, and to extend geometry into the domain of ring theory where the commutative law of multiplication is not assumed.
Another consequence of the contemporary approach, attributable in large measure to the Procrustean bed represented by Bourbakiste axiomatization trying to complete the work of David Hilbert, is to create winners and losers. The Ausdehnungslehre (calculus of extension) of Hermann Grassmann was for many years a mathematical backwater, competing in three dimensions against other popular theories in the area of mathematical physics such as those derived from quaternions. In the shape of general exterior algebra, it became a beneficiary of the Bourbaki presentation of multilinear algebra, and from 1950 onwards has been ubiquitous. In much the same way, Clifford algebra became popular, helped by a 1957 book Geometric Algebra by Emil Artin. The history of 'lost' geometric methods, for example infinitely near points, which were dropped since they did not well fit into the pure mathematical world post-Principia Mathematica, is yet unwritten. The situation is analogous to the expulsion of infinitesimals from differential calculus. As in that case, the concepts may be recovered by fresh approaches and definitions. Those may not be unique: synthetic differential geometry is an approach to infinitesimals from the side of categorical logic, as non-standard analysis is by means of model theory.
History of geometry
The earliest recorded beginnings of geometry can be traced to ancient Mesopotamia, Egypt, and the Indus Valley from around 3000 BCE. Early geometry was a collection of empirically discovered principles concerning lengths, angles, areas, and volumes, which were developed to meet some practical need in surveying, construction, astronomy, and various crafts. The earliest known texts on geometry are the Egyptian Rhind Papyrus and Moscow Papyrus, the Babylonian clay tablets, and the Indian Shulba Sutras, while the Chinese had the work of Mozi, Zhang Heng, and the Nine Chapters on the Mathematical Art, edited by Liu Hui.
Euclid's Elements (c. 300 BCE) was one of the most important early texts on geometry, in which he presented geometry in an ideal axiomatic form, which came to be known as Euclidean geometry. The treatise is not, as is sometimes thought, a compendium of all that Hellenistic mathematicians knew about geometry at that time; rather, it is an elementary introduction to it;[3] Euclid himself wrote eight more advanced books on geometry. We know from other references that Euclid’s was not the first elementary geometry textbook, but the others fell into disuse and were lost.[citation needed]
In the Middle Ages, mathematics in medieval Islam contributed to the development of geometry, especially algebraic geometry[4][5] and geometric algebra.[6] Al-Mahani (b. 853) conceived the idea of reducing geometrical problems such as duplicating the cube to problems in algebra.[5] Thābit ibn Qurra (known as Thebit in Latin) (836-901) dealt with arithmetical operations applied to ratios of geometrical quantities, and contributed to the development of analytic geometry.[7] Omar Khayyám (1048-1131) found geometric solutions to cubic equations, and his extensive studies of the parallel postulate contributed to the development of non-Euclidian geometry.[8] The theorems of Ibn al-Haytham (Alhazen), Omar Khayyam and Nasir al-Din al-Tusi on quadrilaterals, including the Lambert quadrilateral and Saccheri quadrilateral, were the first theorems on elliptical geometry and hyperbolic geometry, and along with their alternative postulates, such as Playfair's axiom, these works had a considerable influence on the development of non-Euclidean geometry among later European geometers, including Witelo, Levi ben Gerson, Alfonso, John Wallis, and Giovanni Girolamo Saccheri.[9]
In the early 17th century, there were two important developments in geometry. The first, and most important, was the creation of analytic geometry, or geometry with coordinates and equations, by René Descartes (1596–1650) and Pierre de Fermat (1601–1665). This was a necessary precursor to the development of calculus and a precise quantitative science of physics. The second geometric development of this period was the systematic study of projective geometry by Girard Desargues (1591–1661). Projective geometry is the study of geometry without measurement, just the study of how points align with each other.
Two developments in geometry in the nineteenth century changed the way it had been studied previously. These were the discovery of non-Euclidean geometries by Lobachevsky, Bolyai and Gauss and of the formulation of symmetry as the central consideration in the Erlangen Programme of Felix Klein (which generalized the Euclidean and non Euclidean geometries). Two of the master geometers of the time were Bernhard Riemann, working primarily with tools from mathematical analysis, and introducing the Riemann surface, and Henri Poincaré, the founder of algebraic topology and the geometric theory of dynamical systems.
As a consequence of these major changes in the conception of geometry, the concept of "space" became something rich and varied, and the natural background for theories as different as complex analysis and classical mechanics. The traditional type of geometry was recognized as that of homogeneous spaces, those spaces which have a sufficient supply of symmetry, so that from point to point they look just the same.
